I’m delighted Ned Nikolov and Karl Zeller have chosen the Talkshop as the venue for the publication of this new open peer review paper on climate sensitivity. Scientific advance at the cutting edge has always been the most important aim of this blog, and I think this paper truly is an advance in our understanding of the climate system and the factors which support and modulate surface temperature on Earth and other rocky planets. 

The paper is mathematically rigorous, but is also accessible to everyone, thanks to Ned and Karl’s exemplary effort to fully explain their concepts and definitions in terms which can be understood by any interested reader who has some familiarity with the climate debate. Building on the bedrock of their 2014 and 2017 papers, this new work extends the applicability and validates the postulates of those previous papers by examining the causes of variability in planetary surface temperature and incorporating the previous findings in quantifying and deriving equations to model them. They find that Earth is sensitive to changes in cloud cover, which affects the amount of solar shortwave radiation reaching the surface, but not very sensitive to changes in Total Solar Irradiance arriving at the top of the atmosphere. They also find that the sensitivity to changes in CO₂ levels has been heavily overestimated by current climate models. They show that a doubling of atmospheric CO₂ concentration from 280 ppm to 560 ppm will cause an undetectable global warming of 0.004K.

A PDF of the paper can be downloaded here:  ECS_Universal_Equations.

______________________________________________________________________

Exact Formulas for Estimating the Equilibrium Climate Sensitivity of Rocky Planets & Moons to Total Solar Irradiance, Absorbed Shortwave Radiation, Planetary Albedo and Surface Atmospheric Pressure.
Ned Nikolov, Ph.D. and Karl Zeller, Ph.D.
April, 2022

1. Introduction

The term “Equilibrium Climate Sensitivity” (ECS) has become a synonym for the steady-state response of global surface temperature to a modeled long-wave radiative forcing caused by a doubling of atmospheric CO₂ concentration with respect to an assumed pre-industrial level of 280 ppm. According to climate models based on the Greenhouse theory, an increase of atmospheric CO₂ from 280 ppm to 560 ppm would produce a net radiative forcing (i.e. an atmospheric radiant-heat trapping) of 3.74 W m^-2 (Gregory et al. 2004) resulting in a global surface warming between 2.5 K and 4.0 K with a central estimate of 3.0 K according to IPCC AR6 (see p. 11 in Climate Change 2021: The Physical Science Basis. Summary for Policymakers). This implies an average unit ECS of 3.0/3.74 = 0.8 K / (W m^-2) with a range of 0.67 ≤ ECS ≤ 1.07 K / (W m^-2). Contemporary climate science and IPCC Assessment Reports do not discuss global temperature sensitivities to changes in cloud albedo, absorbed solar radiation or total surface atmospheric pressure. Consequently, no equations have been derived/proposed thus far to calculate these sensitivities. The reason for such an omission is the implicit assumption made by IPCC based on the 19^th-Century Greenhouse theory (Arrhenius 1896) that the observed warming during most of the 20^th Century and especially over the past 40 years was chiefly caused by an increase of industrial CO₂ emissions, which are believed to trap outgoing long-wave radiation in the Earth’s troposphere and reduce the rate of surface infrared cooling to Space.

However, a plethora of studies published during the past 15 years have shown through both satellite and surface observations that the absorption of solar radiation by the Earth-atmosphere system has increased significantly since 1982 due to a decreased cloud cover/albedo, a phenomenon often referred to as “global brightening” (e.g. Goode & Pallé 2007; Wild 2009; Herman et al. 2013; Stanhill et al. 2014; Hofer et al. 2017; Pfeifroth et al. 2018; Pokrovsky 2019;  Delgado-Bonal et al. 2020; Dübal & Vahrenholt 2021;  Yuan et al. 2021). This implies a global warming driven by a rising surface solar radiation rather than CO₂.

While the CO₂ “radiative forcing” is a model-generated quantity, the brightening of Earth’s surface over the past 4 decades has been inferred from actual instrumental measurements. Nevertheless, the climate sensitivity to variations of shortwave fluxes has largely been ignored by the mainstream science. An a-priori assumption has been made that the sensitivity of global temperature to any type of radiative forcing inside the system should equal the modeled ECS to CO₂. In this article, we’ll show that the Earth’s ECS to shortwave solar radiation is quantitatively quite different from the hypothesized ECS to CO₂. To this end, first we will derive universal analytical models for computing ECS of rocky planets and moons to changes in solar radiation, planetary albedo, and total atmospheric pressure. Secondly, we will verify the albedo-temperature model against CERES satellite measurements of Earth’s reflected shortwave radiation obtained during the past 20 years. Finally, we will apply the new analytical models to compare climate sensitivities of Earth to those of other planetary bodies in the Solar System and discuss reasons for estimated differences.

2. Derivation of Analytical Models of Equilibrium Climate Sensitivities

Analytical models are mathematical expressions with a closed form solution, which means that the solution to a differential equation describing the change of a system’s parameter is exact and can be expressed as a mathematical analytic function.

While analyzing NASA planetary data, Nikolov & Zeller (2017) made a discovery that the long-term (baseline) global surface temperature of rocky planets and moons (T_sb ,K) is mainly a function of two variables: Total Solar Irradiance (TSI) reaching the top of the atmosphere and the mean atmospheric pressure at the surface. In mathematical terms:

where T_na(S) is the global average surface temperature in the absence of atmosphere (i.e. the no-atmosphere temperature), which chiefly depends on TSI (S , W m^-2); and E_a(P) is the Relative Atmospheric Thermal Enhancement (RATE), a dimensionless quantity describing a form of adiabatic heating caused by the gravity-induced force of air pressure (P , Pa). Figure 1 displays the planetary bodies and their observed key parameters utilized in the Dimensional Analysis of Nikolov & Zeller (2017).

Figure 1. Planetary bodies in the Solar System with available high-quality observations of environmental variables used in the Dimensional Analysis of Nikolov & Zeller (2017). Note that A and Ts in this Figure correspond to 𝛼_b and T_sb in the text.

Volokin & ReLlez (2014) showed that the airless global surface temperature of a spherical body is given by the formula:

where 𝛼_e is the albedo of the surface regolith under airless conditions (fraction); η_e is the fraction of absorbed daytime solar radiation stored in the regolith and released as heat at night; R_c = 3.13𝑒 − 6 is the cosmic background radiation (W m^-2); R_g is the average geothermal heat flux at the surface (W m^-2); ε is the regolith long-wave emissivity (≈0.98); and
σ = 5.67e − 8 W m^-2 K^-4 is the Stephen-Boltzmann constant relating the radiative flux from a body to the 4^th power of the body’s absolute temperature. Equation 2 was derived via spherical integration of the Stephen-Boltzmann radiation law.

RATE is calculated using an empirical function derived via non-linear regression analysis of data from 6 planets and moons spanning a vast range of physical conditions in the Solar System (Fig. 1), i.e.

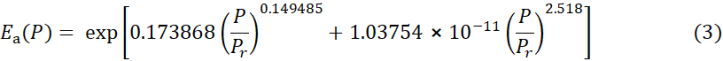
where P_r = 0.61173 kPa is a reference pressure assumed to equal the triple point of water. The purpose of using a reference pressure in Eq. 3 is to make the regression coefficients independent of pressure-measurement units. Note that the empirical coefficients in Eq. 3 differ somewhat from those published by Nikolov & Zeller (2017), because the regression analysis has been updated since the original paper using newer and better data for the baseline planetary temperatures of Venus, Earth, and Titan. Figure 2 depicts the curve described by Eq. 3.

Figure 2. Graphical depiction of the Relative Atmospheric Thermal Effect (RATE), a form of pressure-induced adiabatic heating empirically described by Eq. 3.

A key new insight from the NZ model (Eq. 1) is that the climate system is not solely driven by radiation, which is a form of diabatic (external) heating, but it is also controlled by an adiabatic enhancement of the absorbed solar energy (internal heating) due to air pressure. Adiabatic heating is a standard thermodynamic phenomenon in compressible fluids such as gases. The Greenhouse theory of climate change exclusively focuses on radiative forcing and positive radiative feedbacks, and does not consider the adiabatic warming effect of atmospheric pressure on a planet’s surface.

Nikolov & Zeller (2017) demonstrated that, for bodies with tangible atmospheres, Eq. 2 can be simplified (without sacrificing numerical accuracy) by using constant generic values for 𝛼_e and η_e based on NASA’s Moon data and ignoring the small energy-flux terms R_c and R_g i.e.

This reduces Eq. 1 for planetary bodies with an atmosphere to the following simple expression:

Equation 5 does not contain explicit terms for the absorbed solar radiation or the cloud albedo. Yet, it provides a robust mathematical basis for the derivation of exact analytical formulas to quantify planetary climate sensitivities to incoming shortwave radiation, albedo, and total surface pressure. That’s because this integral model accurately and completely describes the baseline global surface temperature of planetary bodies over a broad range of physical environments in the Solar System (see Figures 1 and 2). As such, Eq. 5 can be combined with the rules of calculus to produce closed-form solutions for various equilibrium climate sensitivities defined in terms of perturbations to the baseline global temperature.

2.1 Modeling the Sensitivity of Global Temperature to Total Solar Irradiance

The sensitivity of T_sb to TSI can be inferred from the total derivative of T_sb with respect to S, dT_sb/dS. Using Eq. 5 in combination with the chain rule of calculus, we obtain:

Since the mean surface atmospheric pressure (P) is a function of gravity and the mass of an atmospheric column above a unit surface area, P can be viewed as being independent of S for small variations of a planet’s orbit around the Sun such as those caused by Milankovitch cycles. This implies ∂P⁄∂S = 0, which reduces Eq. 6a to:

Thus, the total derivative dT_sb/dS becomes equal to the partial derivative of dT_sb with respect to S , which can be obtained by differentiating Eq. 5:

Upon separation of variables and integrating both sides of Eq. 7, one arrives at the expression:

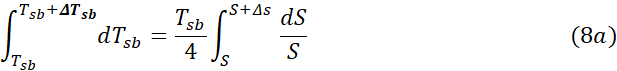
which has the closed-form solution:

In Eq. 8, ΔT_sb is a change of the baseline temperature T_sb caused by a TSI perturbation Δs. Hence, the sensitivity of global temperature to TSI is proportional to the current baseline temperature of a planet and increases logarithmically with the magnitude of the TSI perturbation.

2.2 Modeling the Global Temperature Sensitivity to Absorbed Solar Radiation

The sensitivity of T_sb to absorbed solar radiation (S_a , W m^-2) can be evaluated using a similar approach to the one employed in Section 2.1. Applying the chain rule of calculus to Eq. 5 yields the following expression for the total derivative dT_sb/dS_a :

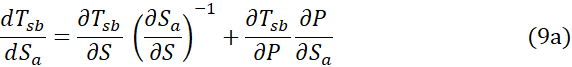
Again, since the mean atmospheric pressure P at the surface is independent of S_a for small variations of the absorbed shortwave flux caused by albedo fluctuations, we can safely assume ∂P/∂S_a = 0 , which simplifies Eq. 9a to:

The partial derivative ∂T_sb/∂S was already evaluated in Eq. 7. The second partial derivative ∂S_a/∂S can be obtained from the standard formula for calculating the average absorption of shortwave radiation by a sphere:

where α_b is the planet’s long-term (baseline) Bond albedo defined as the phase-integrated fraction of incident solar radiation at the top of the atmosphere that is reflected back to Space, and thus lost to the climate system. Differentiating Eq. 10 with respect to S yields:

Combining Equations 7, 9b and 11 produces a differential formula describing ECS to S_a :

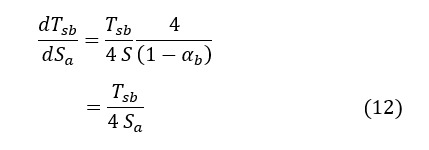
Quantifying the equilibrium temperature response ΔT (K) to a finite change of the absorbed shortwave flux ΔS_a (W m^-2) requires a separation of variables in Eq. 12 followed by integration of both sides, i.e.:

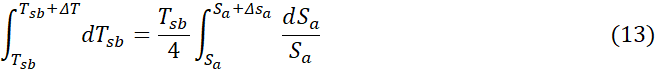
Equation 13 has the closed-form solution:

Replacing S_a in Eq. 14 with its equivalent from Eq. 10 yields the final analytical formula for calculating ΔT as a function of ΔS_a:

In Eq. 15, ΔT is the deviation of global surface temperature from a baseline value T_sb. Similar to the TSI sensitivity, here ΔT is also proportional to T_sb and varies logarithmically with the radiation-absorption perturbation ΔS_a.

2.3 Modeling the Sensitivity of Global Temperature to Planetary Albedo

Since the albedo is a key parameter determining the amount of solar radiation absorbed by a planetary body, we can use Eq. 15 as a starting point to derive a formula for the global temperature response ΔT to a finite albedo perturbation Δα . To this end, first we differentiate Eq. 10 with respect to α_p:

The solution to this is simply

Next, we replace ΔS_a in Eq. 15 with its equivalent from Eq. 17 to arrive at an analytical albedo-temperature formula:

Using Eq. 18 we can now write a mathematically robust expression describing the global surface temperature of a rocky planet or moon (T_s ) as a function of 3 terms: (a) the no-atmosphere global surface temperature T_na(S) being chiefly a function of TSI; (b) the pressure-induced adiabatic atmospheric thermal enhancement E_a(P); and (c) the temperature anomaly ΔT caused by a departure of the planet’s albedo (Δα) from a baseline value α_b (Eq. 18) i.e.

Upon replacing the three terms in Eq. 19 with their equivalent expressions from Equations 2, 3 and 18 we arrive at a generic model describing the average global surface temperature of rocky planets and moons with atmospheres of arbitrary amount and composition:

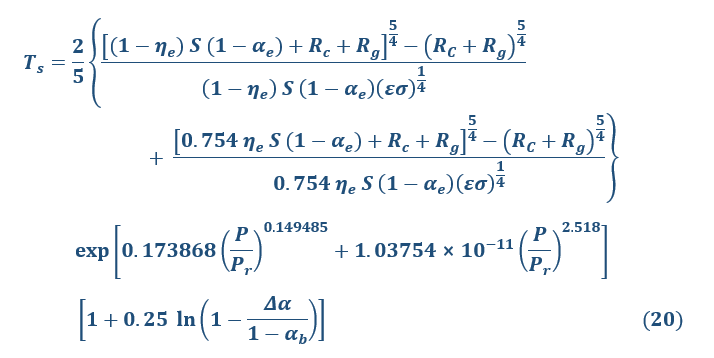
Equations 18 through 20 have important new implications for the role of albedo in planetary climates that can be summarized as follows:

a) TSI and the mean atmospheric pressure at the surface determine the baseline (long-term) global surface temperature (T_sb ) of rocky planets while also giving rise to a baseline albedo . Hence, α_b is a byproduct of the climate system. Being an intrinsic property of that system, α_b does not affect T_sb. This conclusion follows from the 2017 Nikolov-Zeller model (Eq. 1), which accurately describes the long-term global surface temperatures of planetary bodies over a vast range of environments in the Solar System without explicitly accounting for differences in Bond albedos. Vetted NASA observations suggest that, across a broad range of physical environments, α_b cannot be predicted from measured temperatures and atmospheric pressures. This fact further reinforces the notion that α_b is an emergent parameter of the climate system rather than a controller of climate. Such an understanding about the physical nature of α_b explains the observed stability of planetary albedos, since atmospheric pressure and TSI that give rise internally to α_b tend to be stable over long periods of time.

b) If TSI and surface air pressure are constant, then the global surface temperature T_s can deviate from T_sb only if the planet’s cloud albedo is forced to depart from its baseline value. Hence, the albedo only affects a planet’s global temperature if Δα ≠ 0.0. Since Δα is much smaller than α_b due to negative feedbacks operating within the climate system that constrain albedo fluctuations, the bulk of the albedo on any planet or moon with a tangible atmosphere has no impact on T_s. This implies that large positive ice-albedo feedbacks simulated by theoretical models are likely unreal, which is counterintuitive and constitutes a new finding in climate science.

For a more comprehensive discussion about the role of albedo in climate, please watch this video  presented at the 101^st AMS Meeting in January of 2021.

2.4 Modeling the Global Temperature Sensitivity to Total Atmospheric Pressure

Current climate science does not recognize direct thermodynamic effects of atmospheric pressure on the global surface temperature. The “Greenhouse” theory only acknowledges the influence of pressure on temperature through the pressure broadening of gaseous infrared absorption lines. The semi-empirical model by Nikolov & Zeller (2017) is the only one that properly quantifies the Atmospheric Thermal Effect as a form of a pressure-induced adiabatic heating operating on rocky planets and moons with atmospheres. This makes the NZ model uniquely suited for evaluating the climate sensitivity to a change of total air pressure (Δp ). Since the atmospheric thermal enhancement E_a(P ) described by Eq. 3 is an explicit integral function of pressure, one does not need derivatives and the chain rule of calculus to come up with a correct climate-sensitivity model. Instead, one must simply perform a differencing of Eq. 1 with respect to pressure to calculate the climate sensitivity ΔT_sb (K) to this thermodynamic forcing i.e.

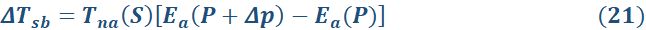
Note that Eq. 21 quantifies the response of the baseline temperature itself to a change of total surface pressure Δp. In contrast, formulas describing climate sensitivities to variations of albedo and the absorbed solar radiation (Equations 15 and 18) evaluate the deviation of global temperature ΔT from a baseline value T_sb. This principal difference is due to the fact that TSI and total atmospheric pressure are the variables defining a planet’s baseline temperature T_sb (Eq. 1).

3. Verification of the Albedo-Temperature Model against CERES EBAF Data

We decided to test the hypothesis that global temperature variations in recent decades were caused by changes in cloud albedo rather than atmospheric CO₂ concentration. To this end, we inverted Eq. 20, which incorporates the new analytic albedo-temperature model (Eq. 18) to estimate monthly and annual changes in Earth’s albedo (Δα ) and the Reflected Solar Flux (RSF) at the top of the atmosphere from observed global near-surface temperature records provided by two official data sets: the satellite-based UAH and the surface-based HadCRUT4. Reported temperature anomalies by UAH and HadCRTU4 were converted to absolute global surface temperatures by assuming that, during the 1981 – 2010 period, the Earth’s average surface air temperature was 287.2 K (Jones & Harpham 2013). A value of 0.3 was used for the baseline albedo in Eq. 20 corresponding to a pre-industrial global baseline temperature of 286.4 K.  TSI was quantified in our model using the AcrimSat observational record. RSF was calculated from modeled Δα using Equations 10 and 17. Next, we compared the modeled dynamics of RSF to reflected shortwave radiation independently measured from orbit by the Clouds and the Earth’s Radiant Energy System (CERES) from 2001 to 2019. We utilized Edition 4.1 of the CERES Energy Balanced and Filled (EBAF) data product. If albedo anomalies (Δα ) predicted by the inverted Eq. 20 (which contain no “greenhouse-gas forcing”) using observed global surface temperatures from two independent sources agree with satellite-measured changes of reflected shortwave radiation by CERES, then our hypothesis would be considered validated.

Figure 3 shows the results from the model-data comparison using smoothed monthly data. Figure 4 illustrates comparison results based on annual data. Note that the modeled reflected solar fluxes fall within one third of the CERES calibration uncertainty range, which indicates a tight functional relationship between the planetary albedo and global surface temperature.

Figure 3. Monthly dynamics of modeled reflected shortwave radiation by Earth based on Eq. 20 and near-surface global temperature records compared to observed reflected shortwave fluxes shifted 7 months forward independently measured by CERES.

Figure 4. Annual dynamics of modeled reflected shortwave radiation by Earth based on Eq. 20 and near-surface global temperature records compared to observed reflected shortwave fluxes independently measured by CERES.

Changes of modeled albedo inferred from near-surface temperature records employing different measurement methods match remarkably well the interannual variation and the multi-year trend of measured reflected solar radiation by CERES. This suggests an albedo control over the global surface temperature variations since 2001. Our analysis also showed that the best model-data match is achieved when reflected CERES shortwave fluxes are shifted 7 months forward. This implies that the global surface temperature responds to changes of cloud albedo with a lag of 7 months. The presence of such a lag further strengthens the argument that observed interannual variations and the overall multidecadal trend of global temperature are indeed driven by changes in Earth’s cloud albedo rather than human CO₂ emissions. Prior published research has shown that Sun’s activity likely forces changes in Earth’s cloud albedo either directly via modulation of the interplanetary electric field by solar wind (Voiculescu et al. 2013) or indirectly through the Sun’s magnetic field constraining the flux of galactic cosmic rays into the Earth’s troposphere. Cosmic rays are known to ionize air molecules and boost the production rate of cloud-condensation nuclei, thus increasing the low-level clouds (Svensmark et al. 2021). Although the exact mechanisms of cloud control by the Sun are not sufficiently understood yet to be mathematically incorporated into climate models, it is becoming increasingly clear that, on a decadal time scale, Earth’s climate is governed by the parameter Δα in Eq. 20, not anthropogenic CO₂. Nevertheless, more research is needed in the area of magnetic/electric interactions between Earth and the Sun, and the effect of such interactions on cloud dynamics. In this regard, it’s important to point out that, according to recent satellite observations, the interplanetary Space is not electrically neutral as previously thought but instead is filled with plasma-enabled electric currents (a.k.a. Birkeland currents) measuring millions and billions of Amperes (see this 2018 EOS article entitled “Electric Currents in Outer Space Run the Show”). Climate models do not simulate the ionizing and electric effects of cosmic rays and the solar wind on cloud dynamics.

The high accuracy of the modeled reflected solar fluxes inferred from two independent global temperature datasets (Figures 3 and 4) validates our hypothesis that Earth’s climate of the 21^st Century is most likely driven by fluctuations of cloud albedo rather than an elusive CO₂ “radiative forcing” inferred from theory.

The above results also indicate that the hereto derived analytical models quantifying equilibrium climate sensitivities to variations of albedo and absorbed solar radiation are mathematically correct and physically robust. In a follow-up article soon to appear on this blog, we will apply Equations 15 and 18 to reassess the evolution of Earth’s global surface temperature over the past 60 years using a new gridded data set of measured Surface Solar Radiation (SSR) produced by Yuan et al. (2021). The article will also analyze the observed increase of SSR (global brightening) since 1982 as a driver of recent global warming.

4. Comparing Equilibrium Climate Sensitivities of Planetary Bodies Across the Solar System

The above results raise confidence in the ability of the new analytical models to correctly quantify the ECS to key forcing agents. This justifies the application of these models to compare equilibrium sensitivities of planetary climates across the Solar System. Table 1 provides such a quantitative comparison for the most studied planetary bodies: Venus, Earth, Moon, Mars, Titan and Triton.

Table 1. Equilibrium Climate Sensitivity (ECS) of planetary bodies in the Solar System to Total Solar Irradiance (TSI), absorbed solar radiation, total albedo, and surface atmospheric pressure. ECS refers to a steady-state change of the global surface temperature in response to a unit forcing.

Physical Parameter	Venus	Earth	Moon	Mars	Titan	Triton
Average Distance to the Sun (AU)	0.7233	1.0	1.0	1.5237	9.582	30.07
Total Solar Irradiance (S, W m-2)	2,602.1	1,361.3	1,361.3	586.4	14.8	1.5
Baseline Global Temperature (Tsb, K)	699.0	287.2	197.4	190.6	93.0	39.0
Baseline Bond Albedo (αb, faction)	0.90	0.293	0.136	0.235	0.265	0.65
Surface Atmospheric Pressure (P, kPa)	9,300	98.55	3e-13	0.6854	146.7	0.004
ECS to TSI: K / (W m-2), Eq. 8b	0.067	0.053	0.036	0.081	1.518	4.966
ECS to Absorbed Solar Radiation: K / (W m-2), Eq. 15	2.666	0.298	0.168	0.423	7.269	20.97
ECS to Total Albedo: K / (0.01 albedo increase), Eq. 18	-18.412	-1.023	-0.575	-0.627	-0.318	-0.283
ECS to Surface Atmos. Pressure: K / kPa, Eq. 21	0.075	0.161	40.053	4.913	0.038	4.33

.
Climate sensitivities show a complex pattern of variation among the studied bodies due to differences in baseline surface temperatures, Bond albedos, and total atmospheric pressures. In general, the ECS to shortwave radiation increases with T_sb and α_b , and decreases with TSI (S). The ECS to pressure variations is high for nearly airless bodies in relatively close proximity to the Sun such as the Moon and progressively declines in a non-linear fashion with P, approaching zero for bodies with massive atmospheres such as Venus or with sizable atmospheres but located far away from the Sun such as Titan. This is explained in part by the strongly nonlinear response of RATE to surface air pressure (see Fig. 2).

The equilibrium sensitivities of Earth’s global temperature to shortwave radiation (i.e. TSI and the absorbed solar flux) are much lower than assumed by the Greenhouse theory based on a modeled ECS to CO₂. This is because climate models simulate numerous positive feedbacks, which are fictitious in nature, that amplify the initial system response to a CO₂ “radiative forcing” between 2 and 4.5 times. However, as demonstrated by Nikolov & Zeller (2017), the real climate system has no measurable sensitivity to ambient CO₂ due to a minute contribution of this trace gas to the total pressure of Earth’s atmosphere. Distinguishing between a theoretical (model-generated) internal forcing and a measured external climate forcing is crucial for advancing our understanding and predictive capabilities. The incoming solar radiation and its dynamic modulation by the water-cloud albedo appear to be the real forcing of Earth’s climate on decadal to centennial time scales. The relatively low ECS of Earth to TSI and absorbed solar radiation ensures a potentially greater stability of our climate compared to that of other planetary bodies such as Mars, Titan and Triton. For example, Earth’s 0.053 K / W m^-2 sensitivity to TSI implies that expected variations of Sun’s luminosity and Earth’s orbit causing annual TSI fluctuations in the order of 1 – 5 W m^-2 did not and will not ever have a significant impact on Earth’s climate. However, the modulation of Earth’s cloud cover affecting the planet’s absorption of solar energy forced either directly by the solar wind or indirectly by the Sun’s magnetic field through its effect on the galactic cosmic ray flux, is expected to have a sizable impact on global temperature that is 4.4 to 10 times greater than the impact of TSI fluctuations alone. This is because Earth’s ECS to absorbed solar radiation is nearly 6 times higher than the sensitivity to TSI, and the decadal variability of shortwave absorption is typically larger than TSI variability. Note in Table 1 that a 1% shift in Earth’s albedo would cause a -1 K change in the global surface temperature. To put this sensitivity into a perspective, consider that, according to the HadCRUT5 surface temperature record, 1 K is just about the entire warming experienced by Earth since 1850, i.e. over a period of 170 years.

The ECS to albedo variations might be an indicator of how strong the internal feedbacks are that maintain (support) the bulk of planetary albedos as an intrinsic property of the system. Among the bodies listed in Table 1, Venus has by far the highest climate sensitivity to albedo perturbations due to its hot surface and a strongly reflective cloud cover (see Eq. 18). This implies that the Venusian albedo is also likely to show the smallest temporal variations among the studied bodies. Earth has the second highest ECS to albedo perturbations suggesting that the albedos of Mars, Titan and Triton might be more dynamic (less stable) on decadal-to-centennial time scales compared to the Earth’s albedo.

The above estimate of Earth’s ECS to total pressure (0.161 K/kPa) can be used to calculate the response of global surface temperature to a doubling of atmospheric CO₂ compared to a preindustrial level of 280 ppm. According to the Nikolov-Zeller discovery about the adiabatic nature of the atmospheric thermal effect, a change in the amount of any gas in the atmosphere (including CO₂) impacts global temperature only through the contribution of such a change to total surface air pressure. In other words, what matters for the global thermal environment at the surface is the partial pressure of gases, not their infrared radiative properties. Thus, a 280 ppm increase of atmospheric CO₂ implies a 0.0276 kPa increase of surface air pressure (i.e. 98.55*280/10⁶ = 0.0276 kPa). Multiplying this perturbation by the ECS to pressure yields the true response of our planet’s global surface temperature to a CO₂ doubling: 0.0276*0.161 = 0.0044 K. This amount of global warming is practically undetectable. Hence, current climate models overestimate the Earth’s global temperature sensitivity to atmospheric CO₂ about 682 times or by 68,100% on average (i.e. 3.0/0.0044 = 681.8).

5. Conclusion

Derivation of exact analytical formulas for estimating the equilibrium climate sensitivities of planetary bodies to shortwave radiative forcing and surface atmospheric pressure was possible thanks to a new robust model of global surface temperature inferred from NASA planetary data by Nikolov & Zeller (2017). The model provides novel insights about the role of albedo in climate and into the physical nature of the Atmospheric Thermal Effect (currently called “greenhouse effect”) as a form of adiabatic heating caused by total pressure that is independent of atmospheric composition. The ECS Equations 8b, 15 and 18 were derived from the NZ model employing standard rules of differentiation and integration in calculus. Previous attempts to estimate ECS have been focused on the Outgoing Long-wave Radiation (OLR) as a temperature controller based on an a-priori assumption in the “greenhouse” theory that the atmosphere warms Earth by impeding the rate of surface radiative cooling to Space, a process also known as radiant-heat trapping or cooling retardation. However, the rate of cooling is never a limiting factor in the energy budget of open systems such as the atmosphere, because reducing cooling requires a form of thermal insulation that either impedes conduction/convection or reflects back thermal radiation. None of these mechanisms are operating in a free atmosphere. Since OLR is an effect (consequence) of atmospheric and surface temperatures, this infrared flux cannot affect such temperatures especially in a thermodynamic environment characterized by uninhibited energy dissipation through turbulent convection and advection. The approach of using OLR to evaluate climate sensitivity yields erroneous results also in part because it relies on fictional (non-physical) parameters such as the “effective radiating temperature” and the “effective emission altitude” (for details, see Volokin & ReLlez 2014). A study by Harde (2017) provides a recent example of employing this flawed approach and obtaining completely incorrect ECS estimates as a result. Focusing on OLR as a climate controller instead of analyzing incoming shortwave fluxes that heat the system diabatically is backward in regard to the chain of physical causality. Earth’s climate is controlled by the amount of absorbed solar energy and the adiabatic enhancement of such energy by atmospheric pressure, not by OLR. Hence, a planet’s global surface temperature is independent of the atmospheric long-wave radiative transfer and the rate of infrared cooling to Space, because these are byproducts of the climate system.

Combining the original NZ model with an analytical formula that quantifies the response of global temperature to albedo perturbations (Eq. 18) produced Eq. 20, which fully describes the global surface temperature of rocky planets and moons without recourse to a greenhouse-gas radiative forcing. The latter is a model-generated quantity based on a conjectural 19^th-Century hypothesis, which is not supported by modern satellite observations. For example, the classical definition of the “greenhouse effect” as a difference of outgoing long-wave fluxes between the surface and the top of the atmosphere (Ramanathan 1989; Schmidt et al. 2010) yields physically nonsensical results over central Antarctica, where the “greenhouse effect” becomes negative (Schmithüsen et al. 2015;  Sejas et al. 2018). However, the actual atmospheric thermal effect over the Earth’s South Pole measured with respect to the thermal environment of the Moon’s airless South Pole is about 144 K (Fig. 5). Hence, the radiative “greenhouse effect” as currently defined has no meaningful relationship to the actual surface warming caused by the presence of an atmosphere. This is not surprising since the “greenhouse effect” was arbitrarily defined by Prof. Veerabhadran (Ram) Ramanathan (at the Scripps Institution of Oceanography, University of California, San Diego) as a radiative flux difference in the 1980s based on nothing else but his a-priori belief that the atmosphere acts as a blanket trapping heat, which is thermodynamically incorrect. An open, convective atmosphere without a lid on top cannot trap heat and does not impede cooling! Prof. Ramanathan admitted contriving his definition of the “greenhouse-effect” in a 2014 paper entitled “Climate Change and Protection of the Habitat: Empirical Evidence for the Greenhouse Effect and Global Warming“ that was published in a periodical of the Vatican City called “Complexity and Analogy in Science: Theoretical, Methodological and Epistemological Aspects“. He erroneously assumed that the difference of thermal radiative fluxes between the surface and the top of the atmosphere measures “the thickness of the greenhouse blanket”.

Figure 5. The atmospheric thermal effect over Central Antarctica evaluated with respect to the airless thermal environment at the South Pole of the Moon.

The ability of Eq. 20 to accurately reproduce a 20-year trend and interannual variability of reflected solar radiation measured by CERES using observed records of near-surface global temperature as input (Figures 3 and 4) constitutes a physical proof that the recent warming was caused by a reduction of cloud albedo, not a rise of greenhouse-gas concentrations as claimed by the IPCC.

The robust derivation of Equations 8b, 15, 18 and 21 makes it meaningful to apply these models to other planetary bodies in the Solar System in order to compare changes in ECSs along a cosmic environmental gradient. Estimates shown in Table 1 indicate that Earth has a relatively low ECS to shortwave radiation compared to other bodies, which makes Earth’s climate perhaps more stable. Earth’s sensitivity to absorbed solar radiation (~0.3 K/W m^-2) is 2.7 times lower than the typical modeled sensitivity to a CO₂ “radiative forcing” (0.8 K/W m^-2). The reality is that the Earth’s ECS to CO₂ is essentially zero due to a minuscule contribution of this gas to the total atmospheric pressure on our planet. It’s also worth mentioning that Earth’s ECS to TSI is about 6 times lower than the planet’s sensitivity to absorbed solar flux. Earth has a relatively high climate sensitivity to variations of cloud albedo (-1.02 K/1% albedo change), which indicates the presence of relatively strong negative feedbacks within the system that tend to stabilize albedo fluctuations. This is good news for our global climate.

A PDF of the paper can be downloaded here:  ECS_Universal_Equations

via Tallbloke’s Talkshop

May 2, 2022, by tallbloke

Ned Nikolov & Karl Zeller: Exact Calculations of Climate Sensitivities Reveal the True Cause of Recent Warming